コラム円周率 | 江戸の数学

どのような半径の円もすべて相似で、「円周の長さ÷直径の長さ」はすべて同じ数値になります。この数値が円周率で、πと呼ばれます。円の面積の計算にもこの定数が登場しますが、分数でも平方根のような根号でも書き表せない、超越数と呼ばれる種類の無理数です。この数は 3.1415926535... と無限に続く小数で、今ではコンピュータを使って小数点以下5兆桁まで計算されています。

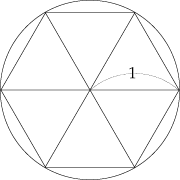$図から、円周は6より大きい。円の直径が2なので、円周率は3より大きい。$ 図から、円周は6より大きい。円の直径が2なので、円周率は3より大きい。

$円周率、最初の1万桁『円周率1000000桁表』$
円周率、最初の1万桁
『円周率1000000桁表』
『円周率1000000桁表』の拡大画像を表示

πの数値については古代各文明で異なるものが使われていました。半径1の円に内接する正六角形の周の長さは6ですので、円周率は3より大きい値であることが分かります。古代エジプトでは正八角形と円を重ねてみることで

$256/81$ (約3.16)

という近似値を得ていますし、古代バビロニアでは

$3+1/8=3.125$

を用いていました。アルキメデスは「円の計測」という著作で

$3+10/71(=3.140845) <π < 3+1/7(=3.1428571)$

という結論を得ました。どういう議論の結果この結論を得たかについては腕試し問題Q14をご覧ください。古代インドで $√10$ =3.1622776 を使った例がありますし、

$62832/20000=3.1416$

を使った例もあります。中国では

$142/45=3.15555$

や

$198/63=3.1428571$

、

$355/113=3.1415929$

などが使われました。こうした無理数の有理数による近似については腕試し問題Q8をご覧ください。
江戸の数学では、吉田光由『塵劫記』(1627)が3.16を使っていますが、この数値は正確でないことが認識され、正確な数値を計算する円理という分野が発達しました。村松茂清、関孝和、鎌田俊清、建部賢弘、松永良弼といった人たちが精密な数値を計算し、ヨーロッパの数学にひけを取らない業績を上げていました。

ヨーロッパでは、ヴィエト(1540-1603)によりπを表わす初めての公式

$2/π＝√(1/2) × √{(1/2)+(1/2)×√(1/2)} x √[(1/2)+[(1/2)×√{(1/2)+(1/2)×√(1/2)}]] x √...$

が発見され、以後、ウォリス(1616-1703)　の公式

$π/2＝(2×2×4×4×6×6×...)/(1×3×3×5×5×7×7×...)$

グレゴリー(1638-1675) ・ライプニッツ(1646-1716)の公式

$π/4＝1-1/3+1/5-1/7+1/9 ...$

などが発見されました。さらにニュートン(1642-1727)やオイラー(1707-1783)により、収束の早い級数が発見され、大きな桁までの計算が可能になりました。また、J.マチン(1680-1752)の発見した

$π/4＝tan-11＝4tan-1(1/5)-tan-1(1/239)$ という関係

を使うと、tan^-1のテーラー展開の最初の4項で3.14159 まで正しい数値が得られます。最近のコンピュータでの計算では

$π＝48tan-1(1/49)-128tan-1(1/57)-20tan-1(1/239)+48 tan-1(1/110443)$

や

$π＝176tan-1(1/57)+28tan-1(1/239)-48tan-1(1/682)+96 tan-1(1/12943)$

という式が使われました。

* tan^-1　アークタンジェント。タンジェント（正接）の逆関数。

和算での円周率の計算

『算法少女』(1775)の巻末に、円周率の計算法が出ています。文章で書いてあることは、原数＝3、

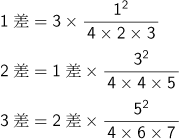
$1差＝3×1 2乗/(4×2×3)、2差＝1差×3 2乗/(4×4×5)、3差＝2差×5 2乗/(4×6×7)$

これを続けて100差まで作る。円周率は、原数＋1差＋2差＋3差＋...である。これを数式に直すと、次のような規則性のある式となると言っています。

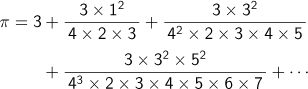
$π＝3＋3×1 2乗/(4×2×3)＋3×3 2乗/(4 2乗×2×3×4×5)＋3×3 2乗×5 2乗/(4 3乗×2×3×4×5×6×7)＋…$

$『算法少女』より「求円周秘術起源」$
『算法少女』より「求円周秘術起源」
この方法は角術も開法も使わない直接的で明快な解法であるとしていますが、どうしてこれが円周率の公式となるかの説明がありません。
国立国会図書館デジタルコレクション
『算法少女』のライブラリーへ移動

この公式は松永良弼の『方円算経』(1739)に書かれているものと同じものです。また、この公式の出し方は忍澄『弧矢弦叩底』(1819)にも載っています。

$『方円算経』より「求周数」$
『方円算経』より「求周数」
円周率(直径1の円周)が小数点以下49桁まで正しく計算されています。
国立国会図書館デジタルコレクション
『方円算経』のライブラリーへ移動

明治に入って、菊池大麓が『東京数学物理学会記事』第7巻(1896)に和算での円周率の計算を紹介する英語論文を4件発表しています。最初の論文は、長谷川弘『算法求積通考』(1844)の計算を紹介したもので、もともと和田寧(1787-1840)が始めた円理豁術という一種の積分計算を、西洋の計算式で説明しています。

$『算法求積通考』より「今有円如図円径一寸問積幾何」$
『算法求積通考』より「今有円如図円径一寸問積幾何」
こちらは直径１の円の面積を出し、4で割って円周率を求めます。この計算には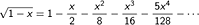 $√(1-x)=1-x/2-x2乗/8-x3乗/16-5x4乗/128- ...$ が利用されています。
国立国会図書館デジタルコレクション
『算法求積通考』のライブラリーへ移動

長谷川は自然数の冪和（ベキ和。累乗の項の和）が、nを大きくすると

$r=1Σnri≒ni+1/(i+1)$

となること(これについては腕試し問題Q6をご覧ください)を使って、

$π/4＝1-1/(2×3)-1/(5×8)-1/(7×16)-5/(9×128)- ...$

という結論を得ていますが、これだけでは規則性がわかりません。実は、各項の間には

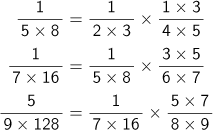
$1/(5×8)= 1/(2×3)×(1×3/4×5)、1/(7×16)= 1/(5×8)×(3×5/6×7)、5/(9×128)= 1/(7×16)×(5×7/8×9)$

というように、前の項に規則的な分数を掛けると次の項が決まるという関係があります。このような級数はK.F.ガウス(1777-1855)が超幾何級数と名付けたものであることに菊池は気づきます。超幾何級数は、

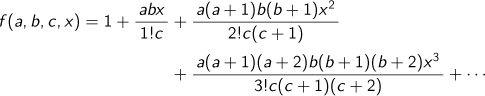
$f(a,b,c,x)=1+abx/1!c+a(a+1)b(b+1)x2乗/2!c(c+1)+a(a+1)(a+2)b(b+1)(b+2)x3乗/3!c(c+1)(c+2)+ …$

で定義されます。

そこで、菊池は次の論文では、和田寧の『円理唇口』での計算

$π＝2(1+1/6+3/40+5/113+ ...)$

は

$π＝2f(1/2,1/2,3/2,1)$

であり、長谷川の計算

$π/4＝1-1/(2×3)-1/(5×8)-1/(7×16)-5/(9×128)- ...$

は

$π/4＝F(1/2,3/2,5/2,1)/3$

であるということ。あるいは松永の

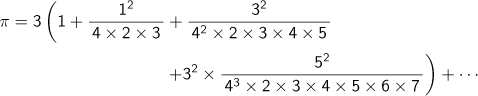
$π＝3(1＋1　2乗/(4×2×3)＋3　2乗/(42×2×3×4×5)＋3　2乗×5　2乗/(4　3乗×2×3×4×5×6×7)＋…)$

は

$π＝3 F(1/2,1/2,3/2,1/4)$

であるということを示しました。

和算では、π^２の計算式を関孝和や建部賢弘らが求めました。建部の導いた

$π２＝9(1+1　2乗/(3×4)+(1　2乗×2　2乗)/(3×4×5×6)+(1　2乗×2　2乗×3　2乗)/(3×4×5×6×7×8)+ …)$

は和算史上で最初の円周率を求める公式です。そして建部はこの式からπを小数点以下41桁まで求めました。菊池は次の論文で、山路主住の『乾坤之巻』(1765頃)にある円の弧sの2乗を矢cと径dで表す式

円の弧と矢と径

$円の弧と矢と径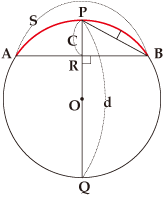$ 図で円周の部分 $APB$ は弧と呼ばれ、線分ABは弦、線分PRは矢と呼ばれます。直径PQは径と呼ばれます。
弧PBに対応する弦を作り、それに対応する矢を作り、とどんどん弦を細かくして行くと、弦をつないだ図形は円に近付いて行きます。こうして、直径がd、矢の長さがcの時の弧の長さsを計算しました。

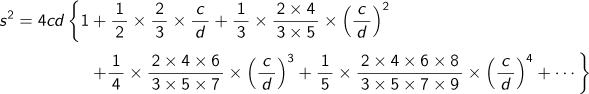
$s2乗=4cd{1+ (1/2)×(2/3)×(c/d) + (1/3)×(2×4)/(3×5)×(c/d)2乗 + (1/4)×(2×4×6)/(3×5×7)×(c/d)3乗 + (1/5)×(2×4×6×8)/(3×5×7×9)×(c/d)4乗 + …}$

を導き出し、

$c=d/2$

の時、

$s=dπ/2$

となることから、

$π２乗＝8{1 + (1/2)×(2/3)×(1/2) + (1/3)×(2×4)/(3×5)×(1/2)2乗 + (1/4)×(2×4×6)/(3×5×7)×(1/2)3乗 + …}=8{1 + (1/2)×(1/3) + (1/3)×(1×2)/(3×5) + (1/4)×(1×2×3)/(3×5×7) + …}$