第2章 関孝和

ここでは3次式 g(x) = x³ + ax² + bx + c を(x - p) で割る場合を考えてみます。筆算すると、

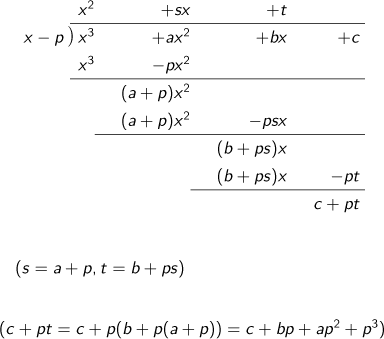
ですので、g(x)を (x－p)で割った商は x² + sx +t = x² + (a + p)x + (b + ps) = x² + (a + p)x + (b + ap + p²)、余りは c + pt = c + p(b + ps) = c + bp + p²(a + p) = c + bp + ap² + p³ -= f(p) となります。
一方、組立除法のやり方を図式化すると

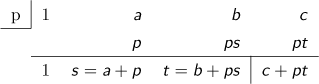
となっており、商の係数、余りが下の行に順番に並んでいます。次数が高くなっても同じアルゴリズムですので、組立除法で商と余りが計算されることが分かります。