腕試し問題（難易度3）

解答　su=t2の証明

解答　su=t2の証明

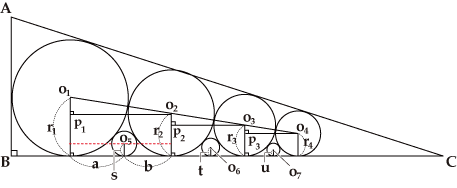
円O1,O2,O3,O4の半径をr1,r2,r3,r4とします。円O1と円O2の位置から(r1-r2)2+(a+b)2=(r1+r2)2、すなわち(a+b)2=4r1r2となります。同様にO1と円O5、円O2と円O5の位置からa2=(r1+s)2-(r1-s)2=4r1s, b2=(r2+s)2-(r2-s)2=4r2s、すなわちa+b=2√(r1r2), a=2√(r1s), b=2√(r2s)、したがって2√(r1r2)=2√(r1s)+2√(r2s)、両辺を2√(r1r2s)で割ると1/√s=1/√r1+1/√r2となります。
同様に1/√t=1/√r2+1/√r3、1/√u=1/√r3+1/√r4となっています。
一方、△O1P1O2,△O2P2O3,△O3P3O4は相似ですので、 (r1-r2)/(r1+r2)=(r2-r3)/(r2+r3)より(r1-r2)(r2+r3)= (r2-r3)(r1+r2)、この式をきれいにしますとr1r3=(r2)2となります。同様にr2r4=(r3)2となり、r1/r2=r2/r3=r3/r4という関係があります。この値をkとすればr1=kr2,r2=kr3,r3=kr4ですのでr1=k3r4, r2=k2r4となります。
上記の関係式を7個の円に適用すると、

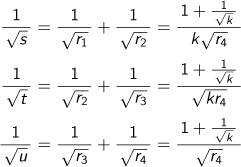
1/√s=1/√r1+1/√r2=(1+1/√k)/k√r4,1/√t=1/√r2+1/√r3=(1+1/√k)/√(kr4),1/√u=1/√r3+1/√r4=(1+1/√k)/√r4

となり、ここからsu=t2となります。

ページ先頭へ